Having discussed the basics of LDPC and error correcting codes in a previous post, this post aims to implement LDPC encoding and decoding using a Python module, pyldpc (Github).

1. Regular vs. Irregular LDPC

Before diving into the code, I want to make a distinction between regular and irregular LDPC codes.

Recall an LDPC code’s parity matrix, \(H\), which defines the number of edges between a variable node and a check node.

Say you want to know how many edges are connected to the first variable node, \(x_1\). You can simply follow the first row of \(H\) and sum the \(1\)’s. Similarly, to find the number of edges connected to the first check node, \(p_1\), you can count the number of \(1\)’s in first column of \(H\). The number of edges connected to a given node is the degree of that node. For variable nodes, the degree of the \(i\)-th node is typically denoted as \(\lambda_i\), and the \(j\)-th check node is typically denoted as \(\rho_j\).

A regular LDPC code has constant degree for all nodes, meaning

for constant, positive integer \(\lambda\) and \(\rho\) where \(n\) is the code length and \(p\) is the number of parity bits. In other words, the degree of the variable nodes are all equal to each other, and the degree of the check nodes are all equal to each other.

In contrast, an irregular LDPC code may assume different degrees of the variable and check nodes may assume different values for different \(i\) and \(j\), respectively. Researchers have shown that irregular codes can achieve better BER at lower SNRs 2. Ultimately, I hope to look into machine learning-based design of irregular codes. However, for this post I will be talking about regular codes.

2. BER of Regular LDPC

To test a given LDPC code, we need an appropriate metric. As an error-correcting code (ECC), the error rate while encoding and decoding under the code is a natural choice. We call this metric the bit-error rate (BER).

So we need to:

1. Generate an LDPC code
2. Generate random messages
3. Encode the messages
4. Add noise
5. Decode the messages
6. Track the number of erroneous messages

Luckily, the pyldpc repo gives a minimal example implementing steps 1-5.

import numpy as np
from pyldpc import make_ldpc, encode, decode, get_message
n = 15
d_v = 4
d_c = 5
snr = 10
H, G = make_ldpc(n, d_v, d_c, systematic=True, sparse=True)
k = G.shape[1]
v = np.random.randint(2, size=k)
y = encode(G, v, snr)
d = decode(H, y, snr, maxiter=100, log=True)
x = get_message(G, d)
assert abs(x - v).sum() == 0

Now to evaluate the generated code, we can sweep across a range of SNR values and check the number of errors.

# encode/decode messages for different SNR vals
mess_num = int(1e3)
tic_incr = mess_num/4
v = np.random.randint(2, size=(mess_num,k))
min_snr=0
max_snr=10
snrs = np.arange(min_snr,max_snr,0.5)
errs = np.array(())
times = np.array(())
for snr in snrs:
    print
    err_num = 0
    time_tot = 0
    current = time.time()
    for i in range(mess_num):
        v_i = v[i,:]
        y = encode(G, v_i, snr)
        d = decode(H, y, snr, maxiter)
        x = get_message(G, d)
        if abs(x-v_i).sum() != 0 :
            err_num = err_num + 1
        if (i+1) % tic_incr == 0:
            time_tot = timer_update(i,current,time_tot,tic_incr)
    err = float(err_num)/mess_num
    print('SNR: {:04.3f}:\n -> BER: {:03.2f}\n -> Total Time: {:03.2f}s'.format(snr,err,time_tot))
    errs=np.append(errs,err)
    times=np.append(times,time_tot)

Notice that I included some timing snippets to keep track of the timing of loop iterations, as decoding was taking a long time at low SNRs. Figure 1 shows the results for BER and Decode Time at each SNR (or \(E_b/N_0\)) for 1000 messages.

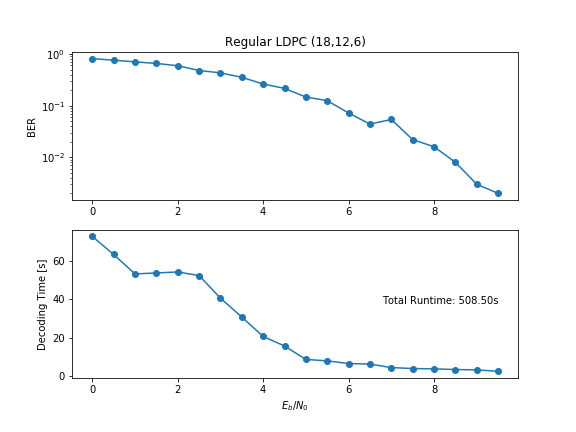
This Gist implements the Python code which was used to produce Figure 1. The LDPC code parameters were chosen somewhat arbitrarily just to get a working example. In [2], the authors used \(n=10^6\) in evaluating codes, but that would have been computationally prohbitive for the purposes of this post.

Moving forward, the pyldpc library will provide a means for evaluating whatever LDPC design methodology we develop.

3. References

• [1]. hichamjanati, pyldpc repository
• [2]. T. J. Richardson, M. A. Shokrollahi and R. L. Urbanke, “Design of capacity-approaching irregular low-density parity-check codes,” in IEEE Transactions on Information Theory, vol. 47, no. 2, pp. 619-637, Feb 2001.